These calendar based on a lunar phase. I had been studied the rules through my grand father’s notes in 1950’s. I had also made a comperhensive study with Javanese and Islamic calendar.

Caka-sunda is the most practical calendar. With a simple calculation, we can make a table which valid for 120 years, earlier 120 years, next 120 years, and so on. This calendar system used as a civil calendar. It is a daily calendar. Historical sunda artefact mostly written in this calendar system.

The month begins from:

perfectly half bright moon - full moon - half dark moon 15 days long, named Suklapaksa

perfectly half dark moon - dark moon - half bright moon 14 or 15 days long, named Kresnapaksa

So the month will segmented in 2 period, 1^st - 15^th Suklapaksa, and 1^st - 14^th/15^th Kresnapaksa. So day 22^nd would be the same as 7^th Kresnapaksa. The Suklapaksa sometimes named ‘paro ca-ang’ (bright parts), and Kresnapaksa somtimes named ‘paro poek’ (dark parts).

Names of Caka-sunda’s month are similar with Saka-india Calendar. But Saka India is a solar system calendar, and its rules are definitely different with Caka-sunda calendar.

The 12^th month (Asuji) will be 29 days long, if it falls on ‘taun pondok’ (short year), and it will be 30 days long, if it falls on ‘taun panjang’ (long years). Those depend on ‘Windu’ (cycle of 8 years) rules:

 The other rule is, the year 8^th should be a short year on 15^th cycles of ‘Windu’, equals with year 120^th (8 years x 15 cycle). 120 years period calls sa-indung poe.

Number of weekdays (= a number of day in 1 cycle) in Caka calendar may varies, from 1 day to 10 days.

Pancawara (5 days per cycle) and Saptawara (7 days per cycle) are mostly used. Those used simultaneously. There are also days name in each weekdays system, but I will write them completely in antoher occasion.

Those name taken from The Star’s name. The ancient Sundanese had also identified planets as stars.

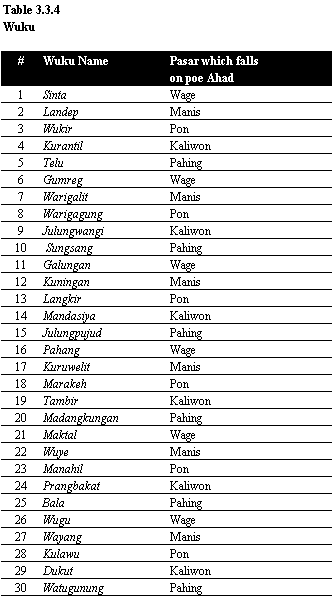
Because of simultaneous use of both Saptawara and Pancawara, it won't be the same 1^st day's-name in a week period, as long as 35 week (in 7 days/week cycle). Wuku or week is a period from Ahad to Saptu. 1^st day name in wuku (=Ahad), usually folows by Pasar (example: Ahad-pon). And every week period has a name (example: Wuku Wukir is a week period which beginning with Ahad pon, refer to table 3.3.4).

With a combination of Indung poe and Naktu (=Neptu in Java Calendar), we can make a calculation to define poe and pasar in a specific date, both in the past and the future. So, if we want to, we don’t need to see a calendar as a table, common format which we daily seen. We just counting just like an example given in section 3.5 below.

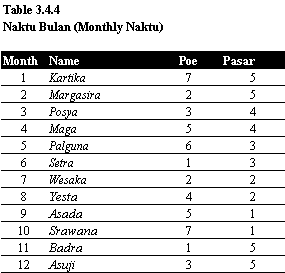
Naktu consist of Naktu pasar (‘5 day/cycle Naktu’, Naktu poe (7 day/cycle (daily) Naktu’), Naktu bulan (monthly Naktu), and Naktu taun (annual Naktu).

Indung poe and Naktu’s origin numbers resulted by caka sunda’s calendar rules. Indung poe and Naktu have strong corelations with Almanac (paririmbon), but for this time, Sunda almanac (paririmbon sunda) is not researched deeply, because I do not find any reliable data.

Detailed of Indung poe and Naktu’s numbers origin will be writen in the next occassion.

Some Sundanese usualy just memorize the rules. Habitually they counting by heart.

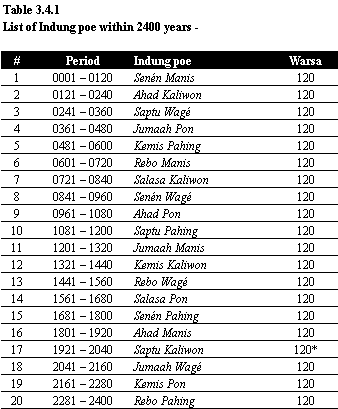
Column # represent the cycle number. This calls Tunggul Taun. Today, year 1998 (Gregorian) is about year 1934 in Caka Sunda Calendar, it should be in a 17^th Tunggul Taun, and an Indung poe which valid is Saptu Kaliwon. This Table is a detailed table for period 1921-2040 or 17^th Tunggul taun;

 Table 3.4.2

17^th Tunggul Taun in Caka sunda calendar

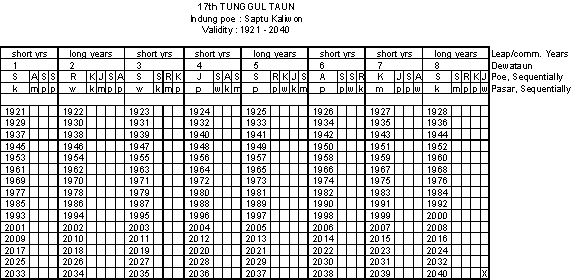
X = 120^th year rules. This year should be a common year only. The next Indung poe will be fall on this day = Jumaah wage. Day sequence (Row #3) : Saptu, Ahad, Senen, Salasa, Rebo, Kemis, Jumaah, Saptu, Ahad,.. Pasar sequence (Row #4): kaliwon, manis, pahing, pon, wage, kaliwon, manis, pahing, …  Example for using this Table : 1^st day on Year 1921 caka (1^st year in this 120 years periodic) fall on Saptu kaliwon. 1^st day on Year 1990 caka falls on Ahad pahing. Year 1925 falls on 5^th Dewataun, year 2040, fals on 8^th Dewataun…

So those results of the addition used to count the poe/day and pasar, starts from indung poe which valid for year 1925 (it is Saptu kaliwon - refer to table 3.4.2)

And then we count sequentially 9 days from Saptu (This day is also included): Saptu, Ahad, Senen, Salasa, Rebo, Kemis, Jumaah, Saptu, Ahad

And for pasar, we count sequentially 7 pasar from Kaliwon (This pasar is also included): Kaliwon, Manis, Pahing, Pon, Legi, Kaliwon, Manis

Because of days/poe are 7 in 1 cycle, we can subtract an additional result more than 7, with 7. In this example is 9 – 7 = 2. Then we count sequentially 2 days from Saptu (This day is also included): Saptu, Ahad

Because of pasar are 5 in 1 cycle, we can subtract an additional result more than 5 with 5, in this example is 7 – 5 = 2. Then we counting sequentially 2 pasar from Kaliwon (This pasar is also included): Kaliwon, Manis

So, 1^st Maga 1925 Caka, falls on Ahad manis

We just counting day and pasar 12 days sequentially from 1^st Maga (=Ahad manis (see an example above)):

Ahad, Senen, Salasa, Rebo, Kemis, Jumaah, Saptu, Ahad, Senen, Salasa, Rebo, Kemis

Manis, pahing, pon, kaliwon, wage, manis, pahing, pon, kaliwon, wage, manis, pahing

For counting day more than 10, some Sundanese usually think in 10 days (or divisible) period/ range. Like this way:

In this example (12^th), they say the day which counting started, twice: Ahad – Ahad, plus 2 days next: Senen, Salasa (it should be totally 10 days from ahad (included)). And then they say the rest of counting (12-10=2 days), rebo, kemis. (They completely say, "Ahad, ahad, senen, salasa – rebo, Kemis")

And for counting days more than 20, 22^nd for example, they will be said:

Ahad, ahad, senen salasa – (and then) Rebo, rebo, kemis, jumaah, - saptu, minggu

After we see those examples, we just need to know which dewataun, naktu taun, naktu bulan and which indung poe should be used. Dewataun and indung poe can be seen in tunggul taun Table (like table 3.4.2) those valid for 120 years. Naktu taun and Naktu bulan will valid as long as Caka sunda calendar with its rules used.